
掛かったコストも、クリックも、獲得したCV件数も全く一緒で、NS0-504 計上された売上のみ異なります。どちらのキャンペーンが結果は良かったかと問われると、間違いなく「Y」になります。
では、どちらに「改善の施し様」があるでしょう。
「G」でしょうか? いいえ、残念ながら、これだけでは解りません。キャンペーンは、NS0-502 無数にあるキーワードと広告で構成されています。この数字は、全てを合算したに過ぎません。
キーワードと広告単位で、CV件数を獲得していないもの、CPAが高いもの、CPCが高いもの等に分類する必要があるでしょう。
しかし、その洗い出しにどれくらいの時間を要するでしょうか。Excel形式で出力した後、全体の数字を見て、何がボトルネックか把握して、何度もエクセルをソートして……。
ずんの飯尾和樹のように現実逃避して、平日の昼間からゴロゴロしながら「あ~あ、中身を全く精査しなくても何となく全体が把握できて、どちらから手を付ければ良いか解らないかなぁ」と呟きたくもなります。
では、そんなことが簡単にできるのでしょうか。できるんです。そう、基本統計量ならね。
「基本統計量」とは何か?
簡単に言うと、基本統計量とは「集団(データ)全体を調べて、特徴・傾向を把握する手法」です。全体を俯瞰し、大まかな形を掴むために最適な解析手法なのです。
基本統計量は、代表値と散布度の2つで構成されます。代表値は「集団の真ん中」を、散布度は「集団の差異(バラつき)」を、たった1つの数値で表現します。
リスティングのおおよそがロングテールだと言われていますが、基本統計量を使えば、獲得した結果の中心が解るだけでなく、どれくらい長い「テール」が続くのかが読めるようになります。
詳細な説明をするより、実際に「基本統計量」を触ってみましょう!
以下の図は、媒体「G」「Y」の広告毎のクリック数になります(同じ広告が、違う媒体に掲載されていたとします)。本当は十数万あることも珍しくないのでしょうが、解り易くするためにそれぞれ10件に絞っています。この数字をもとに進めて行くことにします。
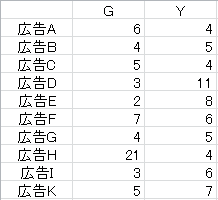
基本統計量はExcelにアドインされているツールで、結果を出すことができます。
[データ]タブを選択後、データ分析を選択してください。そして、いくつかある中から「基本統計量」を選択してください。すると、以下のような選択画面が表示されます。
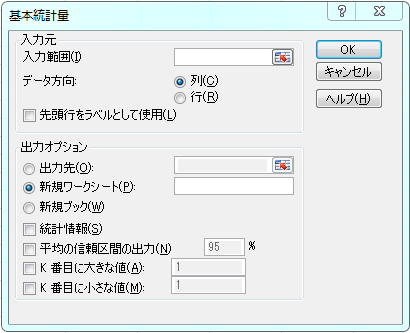
もし、データ分析がなければ、[ファイル]タブのオプションを選択後、[アドイン]-[管理]の設定を選択して、「分析ツール」のチェックを有効にして下さい。
ここで説明した内容はExcel2010を指します。それ以前のバージョンの場合、それに沿った選択をして下さい。
入力範囲は、「対象としたい集団(データ)」を選択します。そして、下側の「統計情報」のみチェックボックスにチェックを入れて下さい。
それだけ入力すると、あとは[OK]を選択するだけです。すると、新規ワークシートに結果が表示されます。ちなみに、媒体Gの基本統計量は以下の通りになりました。
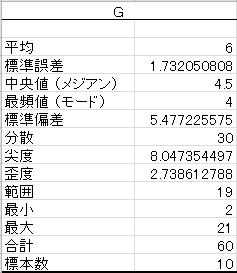
平均や合計などの聞いたことがある単語が並ぶ一方で、分散や標準誤差、尖度、歪度などの聞き馴染みのない単語も並んでいます。
この全てについて把握しておく必要はありません。「平均」「中央値」「標準偏差」「尖度」「歪度」だけで十分です。
代表値から見る「真ん中」はどのあたり?~平均と中央値~
「平均」から説明します。
平均は、皆さんが日常で最も使われている「解析手法」だと思います。「データを足し合わせ、データ数で割った値」を指します。
媒体「G」も媒体「Y」もクリック数の平均は「6」です。ExcelのAVERAGE関数を用いれば答えが表示されます。
![]()
次に、「中央値」です。
中央値は、「データを数値の大きい(小さい)順番に並べたとき、ちょうど真ん中に位置する値」を指します。ちなみに、データ数が偶数の場合は、中央の2つのデータの平均をとります。
媒体「G」のクリック数の中央値は「4.5」、媒体「Y」は「5.5」です。ExcelのMEDIAN関数を用いれば答えが表示されます。
![]()
ところで、平均も中央値も「真ん中を見つける解析手法」ながら、何故かかい離していることが解ります。
その理由は簡単で、データの中に異常に大きい(小さい)データがあるとき、「平均」はそのデータの影響を受けて、大きく(小さく)なってしまうからです。
つまり、平均とは「やじろべえ」の支点のようなものなのです。力点が大きくなるほど、支点はそちらへ寄らなければ、全体のバランスを取ることはできません。一方で中央値とは、支点も力点も無く、ただ単純にデータを並べて、真ん中を指しているのみです。
実際、媒体「G」は平均が「6」ながら、中央値は「4.5」に下がりました。これは広告Hが21クリックと異常に大きいデータだからだと言えます。
代表値から見える「差異」
「標準偏差」から説明します。
標準偏差は、「平均値からの離れ方を平均化した値」を指します。
媒体「G」のクリック数の標準偏差は「5.20」、媒体「Y」は「2.10」です。ExcelのSTDEVP関数を用いれば答えが表示されます。
![]()
この「標準偏差」は、あらゆる解析手法の公式に適用され非常に重要なため、もう少し詳しく解説します。
そもそも、個々のデータから平均を引いた値を「偏差」と言います。例えば、上記10件のクリック数の偏差は以下の通りです。
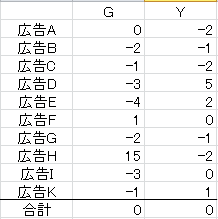
この数値を使えば数値の差異(バラつき)を上手く表現できそうですよね。しかし、単純に足し合わせるだけでは何がどう逆立ちしても「0」になってしまうので意味を成しません。つまり、プラス・マイナスの打ち消しが起きないような工夫が必要なのです。
そこで、「二乗平均」(平均したい数値を、二乗して合計して、個数で割り、その後にルートする)の出番です。二乗することで、マイナスの符号が無くせるので、打ち消し合いも生じません。
ルートにする前の値は「分散」と言います。
ちなみに平均±標準偏差には、全体の6割~7割が入ると考えてかまいません(もろもろ細かい話はありますが、今は忘れて下さい)。つまり、この数字さえ押さえておけば、全体を俯瞰したも一緒なのです。
最後に、「尖度」「歪度」です。
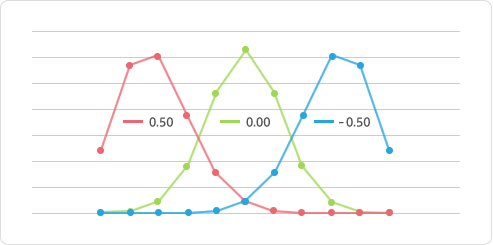
データの分布は、常に正規分布(具体的なイメージはコチラを参照)とは限りません。中心に寄り過ぎたり、逆に裾が広過ぎたり、あるいは峰が左寄りだったり右寄りだったり様々です。そこで「データの分布が上下あるいは左右に、どの程度偏っているかを見る値」のが「尖度」「歪度」です。
媒体「G」のクリック数の尖度は「8.05」、媒体「Y」は「1.98」です。ExcelのKURT関数を用いれば答えが表示されます。
![]()
尖度の場合、値が=0であれば、峰が中央に在ることを示しており、0を上回るほど峰が上に、0を下回るほど峰が下にあることを意味しています。つまり、0を上回るほど、ある一点において量が多いということです。

また、媒体「G」のクリック数の歪度は「2.74」、媒体「Y」は「1.39」です。ExcelのSKEW関数を用いれば答えが表示されます。
![]()
歪度の場合、値が=0であれば、峰が中央に在ることを示しており、0を上回るほど裾峰が右に、0を下回るほど裾峰が左にあることを意味しています。
学んだことをさっそく活かしてみよう!
では今回学んだことを、さっそく復習してみましょう。例えば、CPAをより下げるための施策を打ちたいと考えているとき、どちらの媒体から着手すれば良いか、以下の図から解りますか?
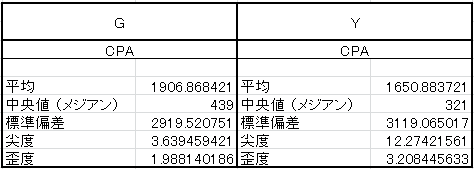
中央値から見て、媒体「G」のほうが明らかにCPAは高いことが解ります。
一方で、平均に標準偏差を足してみると、媒体「G」は1,907+2,920=4,827円、媒体「Y」は1,650+3,119=4,769円と、それほど差が無いことが解ります。
尖度・歪度を見ると、媒体「Y」のほうが媒体「G」と比べて、峰はより上に、裾峰はより左にことが解ります。
つまり、ここから浮かび上がる答えは、
① 媒体「G」は、全体的にCPAが高い。媒体「Y」と比べて、固まって存在している。1から作り直したほうが良い?
② 媒体「Y」は、媒体「G」ほどCPAは高くない。しかし媒体「Y」と比べて、CPAのバラつきはかなり広い。良い広告もあるようなので、既存を活かしつつ悪い広告だけ作り直したほうが良い?
と、媒体に応じた施策が全く違うことが、個々のキーワードや広告のCPAを細かく見なくても、たった10秒で解るのです。今まで、こうした概要を掴むのに、どれほどの時間が掛かったでしょうか。
さらに、定点観測していれば、これだけで十分に全体の概要や改善状況も掴めるはずです―CPAが上がった、下がっただけでは見えない状況が。
まとめ
イギリス元首相ベンジャミン・ディズレーリは、こう言ったとされます。
「嘘には3つの種類がある。 嘘、真っ赤な嘘、そして統計だ。」
なるほど確かに「真ん中を取り出す」と言っても、平均と中央値という手法があり、それぞれ結果が異なる場合もあるのですから、嘘に見えるかもしれません。
しかし、どのような根拠で数字が生まれるかを知れば、我々のようなデジタルマーケッターにとって、こんなにも心強い味方はないはずです。
数字に踊らされず、むしろ数字を踊らせて、様々な分析をこれからも一緒にしていきましょう。
【参考文献】
Excelで学ぶ統計解析入門 著:菅民郎
完全独習統計学入門 著:小島寛之
ご興味のある方は、是非、お問い合わせください。

