今回は数学IAレベルの知識を使って、私のようなファッションに興味の無い非モテエンジニアでも、オシャレでかっこいい服を毎日悩むことなく自動的に選ぶ仕組みを紹介します。
ちなみに中高一貫男子校に通っていた私は、大学生になるまで親に買ってもらった服以外を着たことがありません。服を買うことに興味を持ったことが無いのです。
したがって、私が「生きていく上で困ることランキング」の比較的上位に入っていた項目は「会社に着ていく服を選ぶこと(買うこと)」でした。
このままでは、襟首よれTを着込んで「仙人」という有難くないあだ名がつきかねません。せっかく痩せたのに、見た目がアレでは彼女もできません!何とかしなければ!
http://www.mm-lab.jp/statistical/the_reason_that_was_successful_on_a_diet_in_rizap/
イケてる服選びは神・MBさんに全てを委ねれば良い
「オシャレでかっこいい服を毎日悩むことなく自動的に選ぶ」とは、自宅にイケてる服のストックがある、今日着る服が自動で決まる、この2つが両立しなければなりません。
初っ端から挫折しそうです。どんな服がイケてるか未だによく分からないからです。
「店員に聞けばいいじゃーん!」と言われるのですが、これまで「ショップに足を運べば”何こいつダサい格好で神聖な店来てんだよ”と店員に睨まれている気がする」という理由で、服は全てZOZOTOWNで購入してきました。馴染みの店なんて1つもありません。
したがって、服を選ぶセンスが養われたことがありません。

ご覧の通り、買ってもこんな感じの服です。横ボーダーにピンクのパーカーとか、ピンクパンツにブルーのTシャツとか気狂ってんのか?という感じです。ピンク好きなんです。
ところ、考えてみると「自宅にイケてる服のストックがある」ことと「自分でイケてる服を選ぶ」ことは必ずしも同義ではありません。
そこで友達に教えて貰ったのがMBさんです。以下のサイトを運営されておられます。
http://www.neqwsnet-japan.info/
他にも、こんな本を出版されておられます。

- 縞野やえ MB
- KADOKAWA / 角川書店 2015-12-10

- MB
- 集英社 2017-02-03
ちなみに私は「服を着るならこんなふうに」から入った口で、今では週1回発刊されているメルマガも購読して、とりあえずMBさんが薦めているし…という理由で服を買っています。
ちょうどライザップに通って15kg体重が落ちたので服を買い替えないといけない時期だったこともあり、1年ほどかけて約20万かけて全ての服を買い替えました。
これで、だいたい以下のような服の着こなしに代わりました。

かなり雰囲気変わったと思いませんか。良い意味で落ち着いたというか。自画自賛。
これで「自宅にイケてる服のストックがある」状態はつくれそうです。
「順列」「組み合わせ」で考える服選び
今日着る服が自動で決まるため、数学IAレベルの確率を1から勉強することにします。
まずは「順列」「組み合わせ」を理解するところから始めることにしましょう。
ある物の群から、取り出す順番を考えて取り出して組にしたものが「順列」、考えずに取り出して組にしたものが「組み合わせ」になります。
例えばユニクロUの春夏新作を見て「MEN ミラノリブクルーネックセーター(半袖)めっちゃいいやん!」と思ったとしましょう。色は5色(白、黒、カーキ、オリーブ、青)あるようなので、違う色が3着は欲しいとします。
3着を「選ぶ」となると、考えられる組み合わせは以下の通りです。10パターンです。

では3着を「並べる」となると、どうでしょうか。例えば東京出張が日曜、月曜、火曜にあったとして、どの順番に着るかまで考えるのです。
例えば、白・黒・カーキでは、以下の順番が考えられます。
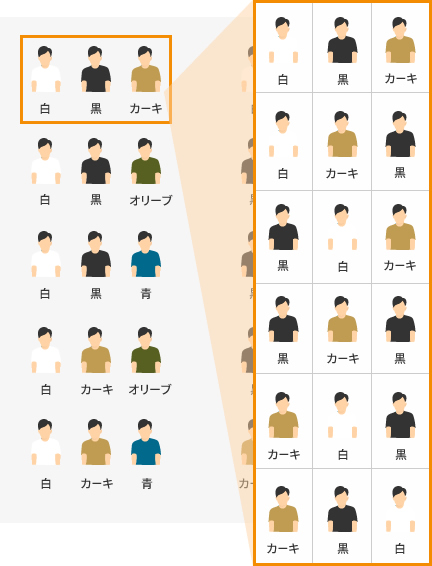
6種類あります。この色の組み合わせが10パターンあるので、順列は6×10=60パターンと分かります。
「組み合わせ総数」×「1つの組み合わせの中の順番」=「順列総数」だと覚えてください。
「n個の中からr個取った”組み合わせ”」をnCrと表現します。
「n個の中からr個取って並べる”並べ方(順列)”」をnPrと表現します。
順列から求めます。
nPr=n×(n-1)(n-2)×…({n-r}+1)=n!/((n-r)!)
今回の例で言えば、5P3ですから、120通りとなります。
いちいち計算するのも面倒なので「5を含む、5からかぞえて小さい数を3つ掛ける」と覚えても良いです。今回の例で言えば、5×4×3=60ですね。
次に組み合わせを求めます。
nCr=nPr÷r! =n!/((n-r)!)÷r!
例えば今回の例で言えば、5C3ですから、10通りとなります。
「nCr×r!=nPr」なので「nCr=nPr÷r!」とも言えるというわけです。
「試行と事象」で考える服選び
次に「試行」「事象」を理解しましょう。
同じ条件で繰り返せて、かつその結果が偶然によって決まる行為を「試行」と言います。代表例がサイコロです(実際には微妙な差があるらしいです)。
そして、試行の結果として起こる事柄を「事象A」、起こりうる結果全ての集合を「全事象U」と言います。
仮に「MEN ミラノリブクルーネックセーター(半袖)」の色違いを5着持っていたとして、今日何を選ぶかは偶然によって決まるとき、白を選ぶことを事象、白・黒・カーキ・オリーブ・青の全てを全事象、そう覚えれば良いでしょう。
そして全事象のうち、1個のみの事象を「根元事象」と言います。例えば「春らしい色を選ぶ」となると白とカーキになりますが、これは1個のみで無いので根元事象ではありません。
最後に、ここが大事な点ですが、ある試行でどの根元事象が起こることも同じく期待できるとき、これらの根元事象を「同様に確からしい」と表現します。
例えば「MEN ミラノリブクルーネックセーター(半袖)」が各色袋の中に1着ずつあって、それを袋の中から1着取り出すとき、どの根元事象が起こるかは同じく期待できるので、これは「同様に確からしい」と言えます。
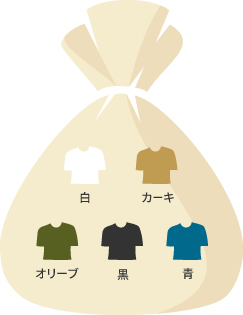
しかし売れ行きが好調過ぎて、袋の中に黒・カーキ・オリーブが無くて、白3枚、青1枚しかなかったとします。このとき「白を袋から取り出す」という根元事象は「同様に確からしい」でしょうか?
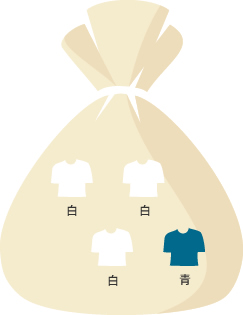
「同様に確か」ではありません。白の方が多いのですから。
しかし、袋の中の白3枚を白1、白2、白3と区別すれば、全事象が{白1}、{白2}、{白3}、{青}なので、白1が取り出せる根元事象は「同様に確からしい」と言えます。

この、「分けて表現」というのが確率の世界ではすごく大事です。
これらのことを踏まえて、確率とは、ある試行におけるある事象の”起こりやすさ”を数値で表したものと言えます。
ある試行において、どの根元事象も「同様に確からしい」とき、全事象Uの個数をn個、事象Aの個数をn個とすると、事象Aの確率P(A)は以下のように表せます。
例えば、上の例で言えば、白1を取り出す確率は「全事象Uの個数が4個」、「事象Aの個数が1個」ですから4分の1になります。
「確率」で考える服選び
さて、私のロッカーにはMBさんがお奨めする服がギッシリあります。
ボトムとトップスの組み合わせを自在に使い分ける勇気は私には無いので、上下一式でセットになっており、この組み合わせを秋冬と春夏それぞれ10種類用意しています。
超簡潔で単純ですが、オシャレでかっこいい服を毎日悩むことなく自動的に選ぶ仕組みとして、この10種類でローテンションをするようなプログラムを作っています。
ただし、毎日同じような服着ていると思われるのは嫌なので、最低1週間は間隔を開けるような「制御」を加えています。
さて、ある冬の日はこんな感じの服装でした。「UNITED TOKYO」好きなんです。

ある月曜日からこのような取り組みを始めるとして、この服装が選ばれる確率はどれくらいあるでしょうか?
全事象Uが10個に対して事象Aが1個なので、確率は10分の1です。
では月曜日は違う服装が選ばれたとして、火曜日にこの服装が選ばれる確率はどれくらいあるでしょうか?
10分の1ではありません。全事象Uは9個になります。最低1週間は間隔を開けるからですね。
確率の問題では「袋に入った玉を1度目取り出して、2度目にさらに取り出すときは、1度目の分を戻さない」というような表現をしています。
確率に基づいて自動的に今日着る服を選べないか?
同じ組み合わせをローテーションで回し続けると、さすがに飽きがきます。そこで勇気を出して、ボトムとトップの分離に挑戦するとしましょう。
しかし毎回闇雲に選んでいては痛い目に遭うので、なるべく重みづけはしたいところです。
そこでボトムを選べば「このトップが似合っていますよ!」と推薦してくれる機能を設けることにしました。ただし、今まで学んだ確率の程度で実装できるレベルです。
まず、重み付けデータの作成から始めましょう。
6種類あるボトムをランダムに選びます。次に10種類ある秋冬向けトップ(シャツorTシャツ+ジャケットの組み合わせ)を選びます。
このランダムに選んだ服装を着てみて「ふつう」「いいやん」「めっちゃいいやん」の3段階で評価します。
「ふつう」であればボール1個、「いいやん」であればボール2個、「めっちゃいいやん」であればボール3個を、服の組み合わせ内容を書いて袋の中に投入するわけですね。
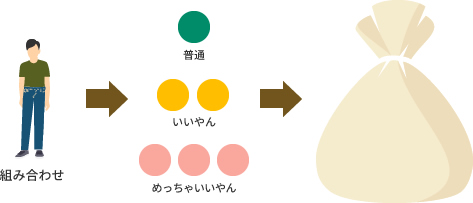
そして60種類のボトム・トップの服装を評価し終えた後、袋の中には最低60個、最大180個のボールが入っているわけです。
さて、ある日、私は「ユニクロのスキニ―ジーンズ黒(腹囲76cm)」を選んだとします。
すると袋の中には、スキニ―ジーンズ黒だった場合に着るトップ10点と、それぞれの評価が書かれたボールが入っているわけです。
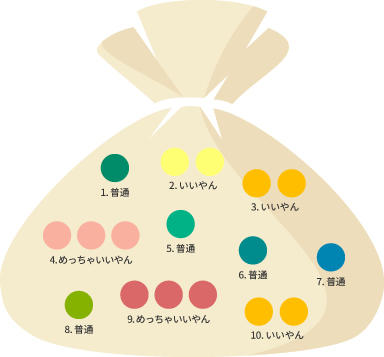
このとき、袋の中には17個のボールが入っているわけですが、「めっちゃいいやん」のトップ2着いずれかが選ばれる確率は全事象17個のうち6個ですから17分の6です。
「いいやん」まで含めた5着だと17分の12ですね。
このとき、各ボールは同じに見えますが、それぞれ区別して考えてください。
それでも「ふつう」の5着が選ばれる確率が17分の5残っているので、それぐらいの確率で「ふつう」が登場するのは嫌だなぁ~と思うならばボール0個にすればいいのです。
すると全事象12個中「めっちゃいいやん」6個となります。服が5着ありますが、「めっちゃいいやん」のトップ2着が選ばれる確率は12分の6すなわち2分の1となるのです。
こうしてオシャレで火傷せずに、素敵な毎日を過ごせそうです。
最後に
ボトムとしてXを選んだ時に…というのは事後確率も応用できそうですが、それはおいおい紹介していくことにします。Step by Step です。
最後に、服装に自信が持てないエンジニアは苦手な領域で努力するよりも、MBさんの力を借りて良い服を選び、余った時間で特異なことをしましょう。
まずは、この本からどうぞ!

- 縞野やえ MB
- KADOK

