今回は、リスティングなどの運用型広告で『今までと違う何かが起きる≒異常』を知らせる検知の仕組みについて考えます。
常時出稿される広告だからこそ「異常」発生の監視は自動化されるべきですが、多くの人が「異常」の基準(閾値設定)に頭を悩ませているはずです。
どこまでが「正常」で、どこからが「異常」なのでしょうか。何をもって境目を見つければいいのでしょうか。
その基準作りは、大量のデータからパターンを見出す機械学習(機械が自動で学習する人工知能研究の一分野)と相性が良さそうです。
つまり過去の傾向からの「違い」を見つけ出し、過去のパターンから作られた一定の基準を超えれば「異常」と見なすのです。
そこで今回は、機械学習を用いた異常検知の方法を調査してみました。Rでのサンプルプログラム付きとなっています。
何をもって「異常」と定義するのか?
業種別マーケティングトレンド予報(16年10月~12月編)でも紹介したこの本をベースに、「異常」の定義をしていきましょう。
本コンテンツに掲載されたコマンドは、この本を参考にしています。凄く分かりやすい本なので購入をオススメします。

- 井手 剛
- コロナ社 2015-02-19
異常検知と聞くとものすごく高度な技術的対応に聞こえますよね。
ただ、端的に説明すると①正常と言えるモデルを過去のデータからつくって、②そのモデルから外れたものを、③外れ具合がある基準を超えれば「異常」とするだけです。
いわゆる「ルールベース」と言われる広告運用では①が人間の経験によって成り立っていました。CPAが1,200円を超えればメールを飛ばす、とかです。
ですが、人間の経験で作るルールベース型の「異常」検知には大きく2つの問題があります。
1.同じ経験を踏まえても人によって捉え方が違う。(INは同じでもOUTが違う)
2.ルールの多様性には限界がある。
1.なんかは極めると職人が誕生しそうですが、膨大な経験と時間が必要そうです。
なにより広告主に対する説明責任という観点では「職人の◎◎さんがCPA1,200円以上は変だと言ったから」では納得して貰えないでしょう。
2.は言い換えると「人間の考えることには限界がある」と同義です。先入観と思い込みが、ルールという人間の思考の塊の広がりを阻害します。
もっとも今回紹介する異常検知の方法も「これが絶対正しい!」というものでもなく、ケースバイケースだし、状況によっては適応しがたいこともあると思います。
以降の異常検知の説明は、イメージし易いようにCPAをKPIに設定している体で話を進めていきます。
データの準備
まず意図的に1地点だけ大きいデータを生成します。Rを使います。
## 正規分布なデータの作成
cpa.a <- rnorm(80, mean=1300, sd=200)
cpa.3σ<- 2100
cpa.b <- rnorm(19, mean=1300, sd=200)
a <- length(cpa.a)
b <- length(cpa.b)
cpa[a+1] <- cpa.3σ
for (i in 1:b) {
cpa[i+a+1] <- cpa.b[i]
}
cpa.df <- data.frame(cpa=cpa.a)
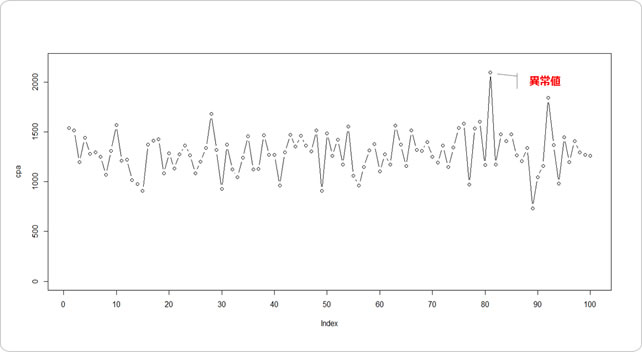
ちなみに、あえてここで完全にランダムなデータではなく正規乱数を使った理由として、CPAは一定範囲内に収まるようコントロールされたデータなので、多少のホワイトノイズは含まれても、正規分布に近い形に収まるのでは?と感じているからです。
私の感覚だとCPAがN円と設定されていれば、日毎のCPAはN±N*20%円、週毎のCPAはN±N*10%円を基準に正規分布している感じです。
コントロールしようとして、コントロールに失敗することもある(≒異常)から、それを発見することが主目的になるかな、と思います。
もちろん全てが全てそうではあると思っていないですし、CPA改善中は適さない等も考えられる(後述)ので、あくまで「仕組みを分かりやすく説明するためにそうした」として受け止めてください。
CPA改善中の場合の異常検知方法については、後半に記述しています。
|x-μ| > 3σ で考える
データが特定基準範囲を上下ウロウロしているのであれば、平均との差分が3σ(標準偏差)を超えるかどうかで見てもいいのではないでしょうか。
Rを使って表現してみます。
## 平均 mu <- mean(cpa.df$cpa) ## 標準偏差 sd <- sd(cpa.df$cpa) cpa.df$mu <- mu cpa.df$plus.sd <- mu + sd*3 cpa.df$minus.sd <- mu - sd*3 # plotする plot(cpa.df$cpa, ann=F, type="b",ylim=c(0,2200), xaxp=c(0,100,10), col="red") par(new=T) plot(cpa.df$mu, ann=F, type="l",ylim=c(0,2200)) par(new=T) plot(cpa.df$plus.sd, ann=F, type="l",ylim=c(0,2200)) par(new=T) plot(cpa.df$minus.sd,ann=F, type="l",ylim=c(0,2200))
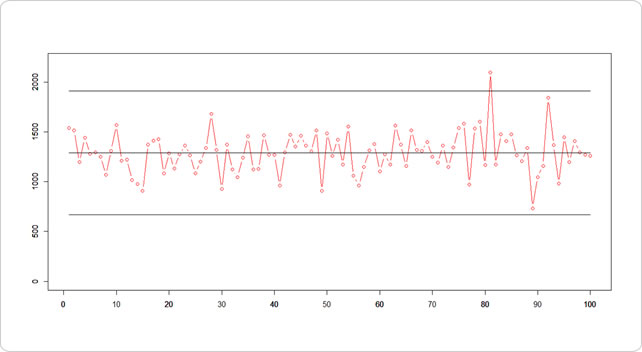
±3σに入る確率は約99.7%ですから、1000日分のデータがあって3日起きるか起きないかの出来事です。
それを超えた値は「外れ値」と見なして、「ちょっと変だよね」と思うに十分ではないでしょうか。
ホテリング理論で考える
次にホテリング理論(正常データ群があって、新しくデータ x を観測したとする。x も正常データ群と同じ分布にしたがうとすると、(x−μ)2/σ2 は自由度 (1,N−1) のF分布にしたがう)で考えます。
ホテリング理論は異常検知技術で最も有名で、最も古典的な手法の1つです。ある観測値x’がどのくらい異常かを表す値α(x’)を定義するだけです。このような計算式で表せます。
α(x’) = ((x’ – μ)/σ)2
観測値x’がある値だった場合に「そのような値をとる確率は1%しかない、だから異常値だと思われる」と、分析者の勘と経験に拠らずに主張できます。
Rを使って表現します。
s2 <- mean((cpa.df$cpa - mu)^2) er <- (cpa.df$cpa - mu)^2/s2 th <- qchisq(0.99, 1) plot(er, xaxp=c(0,100,10)) lines(0:100,rep(th,length(0:100)),col="red",lty=2)
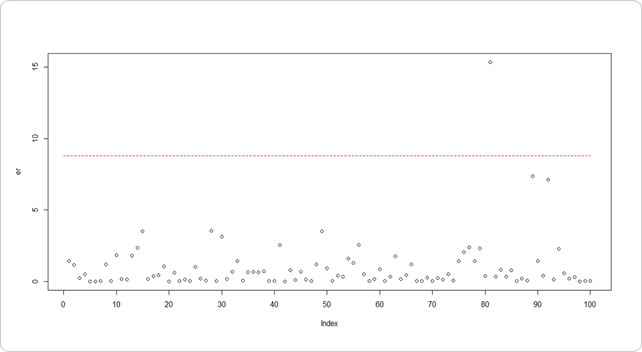
1%水準で考えて、同じく81時点目が異常として検出できました。
ちなみに、訓練データと検証データが同一という点で厳密に言えば使い方が間違っています(本にも記載がありました)。分かれていた方が良いのですが、標本数が多ければ問題無いという見方もあるので、このまま紹介しました。
「異常」は、なるべく少量の標本で、できるだけ正確に検知したいと誰もが思うものです。
それなのに訓練データと検証データを別々に用意しないといけないのは、ちょっと辛いですよね。
ホテリング理論においては「正規分布を前提とするため、正規分布から外れる、分布が複数の山から成るなどの場合は異常値を正しく判断できない」「異常値の定義が一定の平均値からのズレなので、その平均値が動的に変化する場合は検出が困難である」といった意見があります。
したがって最近ではMT法が用いられることが多いようですが、基本的な考え方はホテリング理論に立脚しているので紹介しました。
近傍法による異常部位検出
今までの検知法は、時系列の順番を無視して各時点単位でデータを見ており、時系列データ特有の「並び」を意識していません。
そこで時系列データから異常度を計算する方法としてポピュラーな近傍法を紹介します。
訓練データと検証データに分けて(今回はさすがに!)、それぞれ同じ窓幅の部分的な時系列データを取り出し、そのデータ同士の近傍距離を計算します。
Rを使って表現します。
install.packages("FNN")
library(FNN)
day<- 5
nk <- 1
# 訓練データ
cpa.bf2 <- data.frame(cpa=cpa.df[1:50,])
# 検証データ
cpa.af2 <- data.frame(cpa=cpa.df[51:100,])
d.em.bf2 <- embed(cpa.bf2$cpa,day)
d.em.af2 <- embed(cpa.af2$cpa,day)
cpa.d <- knnx.dist(d.em.bf2,d.em.af2,k=nk)
a <- cpa.d[,1]
par(mfrow=c(1,2))
plot(cpa.bf2$cpa,type="b",ylim=c(0,2000))
plot(cpa.af2$cpa[5:50],type="b",ylim=c(0,2200))
par(new=T)
plot(a,type="l", col="red",ylim=c(0,2200))
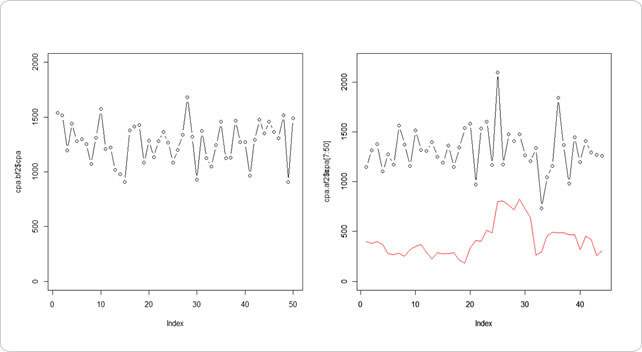
左が訓練データ、右が検証データです。赤線を見てみると、突出した点を検知して異常値が上がっているのと、それに合わせて次の5地点分まで異常であることが分かっています。
これは窓幅に拠ると思います。
傾きを持った時系列データの場合
今までは、横ばいで推移するCPAをベースに考えてきました。
今度は運用改善中で緩やかに落ちていくCPAをベースに考えてみましょう。
cpa.df.Redu <- NULL
for (i in 1:100) {
cpa.df.Redu[i] <- (1000 - i * 10) + cpa.df$cpa[i]
}
cpa.df.Redu = data.frame(cpa = cpa.df.Redu)
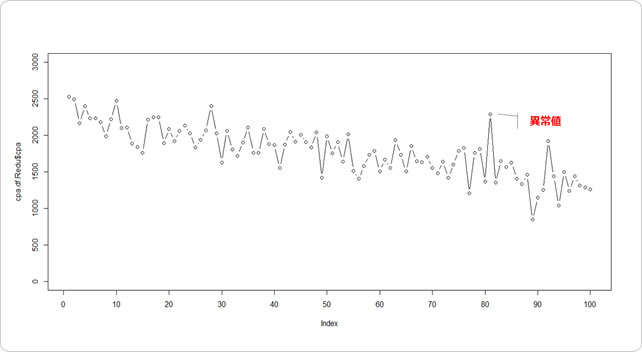
地点毎にCPAが10円ずつ減っていっております。
さて、このデータで今まで紹介した手法で異常を検知できるでしょうか?
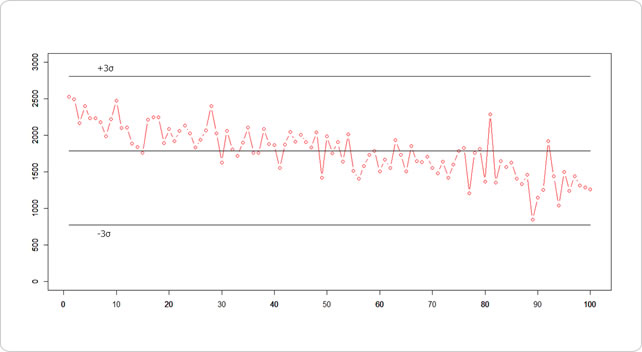
緩やかに右肩下がりなので、σはそりゃ横ばいと比べて大きいですよね。
全てがすっぽりキレイにおさまりました。
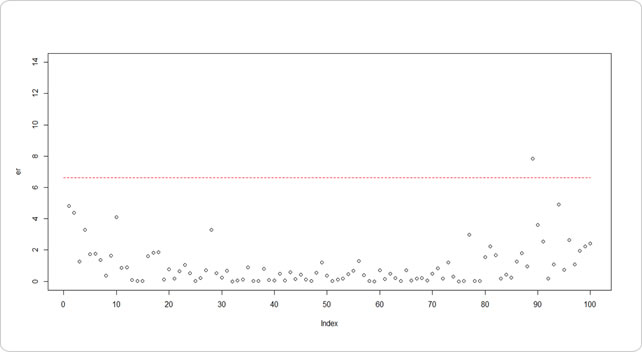
ホテリング統計量もU字型を描いています。先述したように「地点が増える毎に平均値が動的に変化する場合」に該当するので、平均から離れた値ほど異常値になります。
むしろ関係ない89地点目が異常値扱い…。
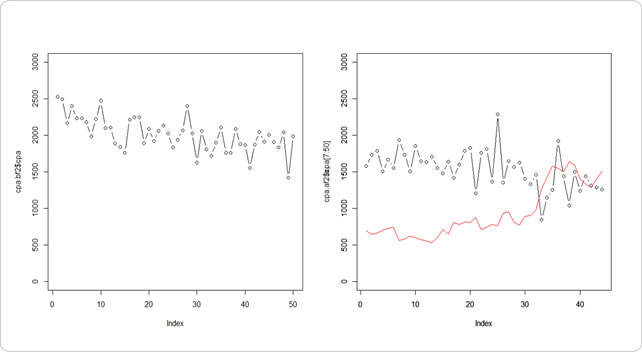
近傍法も同じです。
代替案:回帰直線を引いて異常検知
明らかに右肩下がり(上がり)な傾向が見て取れる場合は、回帰直線を引いて、その直線±3σを見ても良いのではないかと考えます。
Rを使って表現します。
# 線形モデルによる回帰 lm_out<-lm(cpa.df2$cpa~cpa.id) summary(lm_out) coeff<-coefficients(lm_out) # 予測モデルを用いて、全期間の予測(pred)を行う cpa.df2$pred<-coeff[1]+coeff[2]*cpa.id cpa.df2$plus.sd<-cpa.df2$pred+sd(resid(lm_out))*3 cpa.df2$minus.sd<-cpa.df2$pred-sd(resid(lm_out))*3 # 予測と実際を描いて plot(cpa.df2$pred, ann=F, type = "l", ylim=c(0, 3000)) par(new=T) plot(cpa.df2$plus.sd, ann=F, type = "l", ylim=c(0, 3000)) par(new=T) plot(cpa.df2$minus.sd, ann=F, type = "l", ylim=c(0, 3000)) par(new=T) plot(cpa.df2$cpa, ann=F, type="b",ylim=c(0,3000), xaxp=c(0,100,10), col="red")
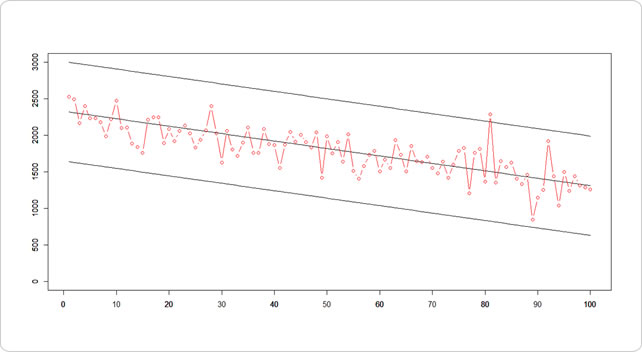
81地点目は、外れ値と見なしても良いということになります。
ただ、ずっと右肩下がりでもないでしょうから、その境目を知らないといかんと思います。
それは異常検知の中でも変化点検知に当たり、こちらの「逐次確率比検定でマメ研が急成長を始めた日を分析する」というコンテンツで紹介しています。
代替案:自己回帰モデルによる異常検知
さらに、この回帰モデルを発展させて、次数rの自己回帰モデルを用います。最適次数についてはAICを用いましょう。
Rを使って表現します。
# 訓練データ cpa.bf2 <- cpa.df.Redu$cpa[1:50] # 検証データ cpa.af2 <- cpa.df.Redu$cpa[51:100] ar.model <- ar(cpa.bf2) print(ar.model) X <- t(embed(cpa.af2-ar.model$x.mean,ar.model$order))[,1:(length(cpa.af2) - r)] yped <- t(X) %*% ar.model$ar + ar.model$x.mean y <- cpa.af2[(1+r):length(cpa.af2)] a <- (y - as.numeric(yped))^2/ar.model$var.pred par(mfrow=c(1,2)) plot(cpa.bf2[1:50],ann=F, type="b",ylim=c(0, 3000)) plot(cpa.af2[r:50],ann=F, type="b",ylim=c(0, 3000)) par(new=T) plot(a,ann=F, type = "l", axes = FALSE,col="red") axis(4)
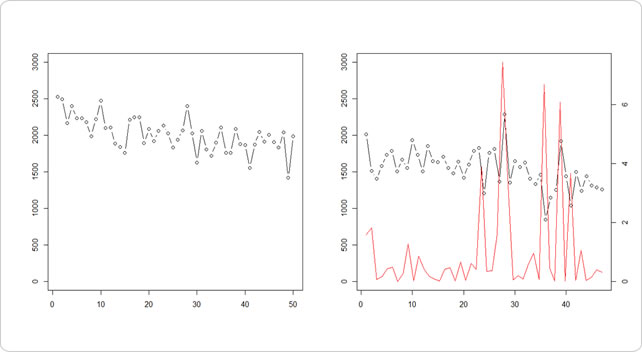
後半が比較的凸凹していたので、違う地点も多く引っかかっていますね…。
もしかしたら、どっかミスってるんでしょうか。
今回のまとめ
なるべく少量の標本で、できるだけ正確に異常を検知する。
この両方のバランスを保とうとするほど、どっちつかずの状態を迎えそうです。
対象期間を長くしてデータ量を多く集めて正確性を担保するか、対象期間が短い代わりに正確性に目をつぶって誤検知を許容するか、このどちらかに寄せたほうが良いでしょう。
手法についても色々と検討しました。
今のところ、私自身がライトに、かつマーケターの方が見て腹落ち度が高いのが(ここは結構重要ではなかろうか)回帰直線を引く手法です。
今回はマーケティング系データに絞りましたが、システムの異常検知や0%~100%の間のシステム閾値設定など、様々な異常検知パターンがあると思います。
このあたりは今後の研究課題としたいですね。
以上、お手数ですがよろしくお願いいたします。

