所長が生まれた頃から「月額課金」「年会費」という課金形態はあったと思うのですが、それにしてもここ数年でいっきに増えましたよね。
最近では月額課金ラーメンの可能性も語られており、そのうち定額制風俗、1授業100円予備校、1曲10円カラオケとかも出てきそうですね。
http://diamond.jp/articles/-/115056
ビジネスモデルが変わると、追うべきKPIも変わります。サブスクリプションの場合は「解約率」ではないでしょうか。
というわけで、今回は「解約率分析」について考えたいと思います。
前段:なぜ解約率を下げることが大事なのか?
従来の売り切りとは違い、サブスクリプションはユーザーの継続的な利用を前提としているので、いかに顧客と長期的な関係を構築できるかが大切だと言われています。
このあたりの詳しいビジネスモデルの解説はググって貰うとして、簡単に言えば、買うと云十万する製品が月額何千円で利用できるのがサブスクリプションというビジネスモデルです。
課金形態は様々ありますが、主に「定額制」「使った分だけ」が主流かと考えます。
ユーザーの利用期間が長ければ長いほど、元が取れて、やがて利益が出てくるビジネスモデルなので、そもそも元が取れないタイミングでの解約は非常に辛い。
つまりXか月目の解約率Y%以内という数字がKPIになりやすいのです。
この人口減少時代、いかに低い単価で新規顧客を獲得するか?という争奪戦から、いかに長い期間顧客で居続けて貰うか?という育成戦にルールが変わっている今、解約率を下げる要因探しは非常に重要な分析だと思います。
生存期間分析を用いた解約率の分析
解約率とは、ある時点で解約した数/ある時点での総数で求まります。
例えば月額課金であれば、X月時点の解約ユーザー数 ÷ X月時点の全ユーザー数(X月以降も利用するユーザー数+X月時点の解約ユーザー数)で解約率が求まります。
しかし全数で見ると様々な要因が隠れてしまうので、改善しようがありません。せめて層別には表現したいところです。
特にサブスクリプションの場合、X月時点の解約率ではなく、利用Xか月目の解約率を見たいはずです。X月時点解約率はユーザーによって利用何か月目か違っているので全く意味をなさないでしょう。
そこでKaplan-Meier法による生存期間分析という、イベント発生までの時間に関する分析法を代替として用いたいと思います。
「○○がん5年後生存率はステージⅡなら30%だけど、ステージⅣなら5%だ」みたいな数字を聞いたことはないでしょうか。ある一定の期間が経過した集団が、その時点で生存している割合を「生存率」と言い、その生存率の算出は生存期間分析で求まります。
生存とか死亡とか表現が恐ろしいですが、イベントの例題なだけで、機械の故障、会社の倒産、製品の打ち切りなど、様々応用が可能です。もちろん「解約」にも。
Rを使って分析してみましょう。
> library(survival); > library(MASS); > data(gehan); > head(gehan); pair time cens treat 1 1 1 1 control 2 1 10 1 6-MP 3 2 22 1 control 4 2 7 1 6-MP 5 3 3 1 control 6 3 32 0 6-MP
マーケティング向けのデータが無いので、生存期間分析向けのデータを用います。
Gehanは生存期間データの1つで、白血病患者に対する薬の効果を調べるために被験者42名に対して行った臨床試験データだそうです。
被験者は薬を投与された人、投与されていない人のペアで構成されています。変数pairがそれに該当します。変数timeは生存期間、変数censは打ち切り状況(0が打ち切り、1が死亡)、変数treatは投与状況を表します。
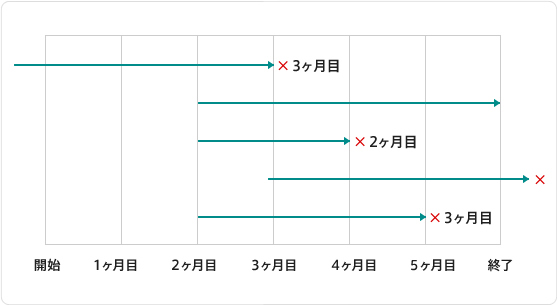
打ち切りには2種類あります。開始から終了までのNか月分ずっとイベントが発生しなかった場合。次に、イベントが発生したわけではないけど途中で離脱など観測が継続できなかった場合。
解約というイベントを分析する場合、後者は気にする必要が無いでしょう。
マーケティング向けに使うなら、人単位に、申込月(日)、解約月(日)、生存期間、打ち切り状況(1がイベント発生)を用意して、使っているサポートランクや契約ステータス等を追加の変数として加えても良いかもしれません。
さて、このデータを関数に当てはめて実行します。Rを使って分析してみましょう。
> sf<-survfit(Surv(time,cens)~treat, data=gehan)
> summary(ge.sf)
treat=6-MP
time n.risk n.event survival std.err lower 95% CI upper 95% CI
6 21 3 0.857 0.0764 0.720 1.000
7 17 1 0.807 0.0869 0.653 0.996
10 15 1 0.753 0.0963 0.586 0.968
13 12 1 0.690 0.1068 0.510 0.935
16 11 1 0.627 0.1141 0.439 0.896
22 7 1 0.538 0.1282 0.337 0.858
23 6 1 0.448 0.1346 0.249 0.807
treat=control
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 21 2 0.9048 0.0641 0.78754 1.000
2 19 2 0.8095 0.0857 0.65785 0.996
3 17 1 0.7619 0.0929 0.59988 0.968
4 16 2 0.6667 0.1029 0.49268 0.902
5 14 2 0.5714 0.1080 0.39455 0.828
8 12 4 0.3810 0.1060 0.22085 0.657
11 8 2 0.2857 0.0986 0.14529 0.562
12 6 2 0.1905 0.0857 0.07887 0.460
15 4 1 0.1429 0.0764 0.05011 0.407
17 3 1 0.0952 0.0641 0.02549 0.356
22 2 1 0.0476 0.0465 0.00703 0.322
23 1 1 0.0000 NaN NA NA
左から各標本の生存時間(time)、その時点で生きている標本(n.risk)、その時点でイベントが起きた標本(n.event)、推定された生存確率(survival)、標準誤差(std.error)、95%信頼区間上下限値になります。
6時点で21標本あって3標本にイベントがある、でも次の7時点では17標本になっています。21-3で18標本じゃないの?と思われるかもしれません。
これはデータの中にtimeが6でcensが0のデータが1件あるからです。2種類ある打ち切りの1つですね。
ところで、この7時点の生存確率が0.807になっていますが、7時点目の死亡は4件なので1-4/21=0.810が正解じゃないの?と考える人もいるかと思います。
勘違いする方もいますが、この生存確率はその時点での累積生存率を表しています。すなわち{1-(3/21)}×{1-(1/17)}=0.807です。要は先ほどの打ち切りの件を考慮しよう!ということですね。
さて、このsurvivalの結果を図にプロットします。
plot(ge.sf,mark.t=T,conf.int=TRUE,col=c("red","green"))
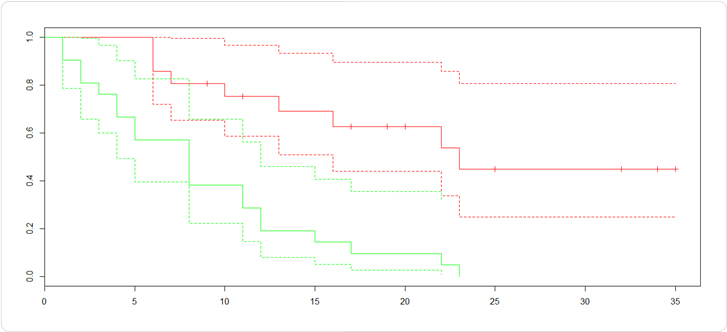
この曲線をカプラン・マイヤー生存曲線とも呼ぶようです。直線が「survival」、上下点線が「lower(upper) 95% CI」になります。
redが「6-MP」で、greenが「control」です。図中に縦棒線がありますが、これは打ち切り時点を表しています。
えらい差が開いていますね…。
この差が有意と言えるかどうかは、ログ・ランク検定法で確認できます。帰無仮説が「差は無い」、対立仮説が「差はある」となるでしょう。Rを使って分析してみましょう。
survdiff(Surv(time)~treat,data=gehan)
N Observed Expected (O-E)^2/E (O-E)^2/V
treat=6-MP 21 21 29.2 2.31 8.97
treat=control 21 21 12.8 5.27 8.97
Chisq= 9 on 1 degrees of freedom, p=0.00275
P値が0.00275なので、有意水準5%水準で帰無仮説は棄却され、両群には有意な差が無いとは言えない⇒差があるのだろう、ということになります。
ちなみに、今回紹介している手法はノンパラメトリックモデル(特定の確率分布を仮定しないし時間以外の共変量を導入しない場合)であり、これ以外にセミノンパラメトリックモデル(分布は仮定しないが共変量を導入する場合)やパラメトリックモデル(分布は仮定するし共変量を導入する場合)があります。
サブスクリプションなどの時間軸による解約率を行う場合、ノンパラメトリック⇒セミノンパラメトリック(コックス比例ハザードモデル)が一般的かもしれません。が冗長になるので割愛します。金教授の本を参考にされるか、以下のページを読んでみると良いかと思われます。
https://www1.doshisha.ac.jp/~mjin/R/37/37.html
時系列な解約率の変化を見てみよう
例えば2016年1月~12月の1年間を対象に、契約から12か月以内の生存確率がどのように変化するか見たとします。こんな感じ。(データはダミーです)
もし、データサイエンティストである貴方がこの結果を責任部署に提示したとして、出てくる答えって以下の場合が多いのではないでしょうか。
「X年Y月からサポート人員を強化しているので、今もこの生存確率とは思えないんです(だから余計なことすんな)」
こういう場合、時系列な生存確率を提案した方が良いかもしれません。
すなわち、2015年1月~12月、2015年2月~2016年1月、2015年3月~2016年2月と1か月単位で時間をズラしながら、当該期間内におけるNか月以内の生存確率を算出するのです。
この場合、月毎のカプラン・マイヤー生存曲線を作成するより、Nか月目の生存確率を時系列なグラフにプロットすることをお勧めします。こんな感じです。(データはダミーです)
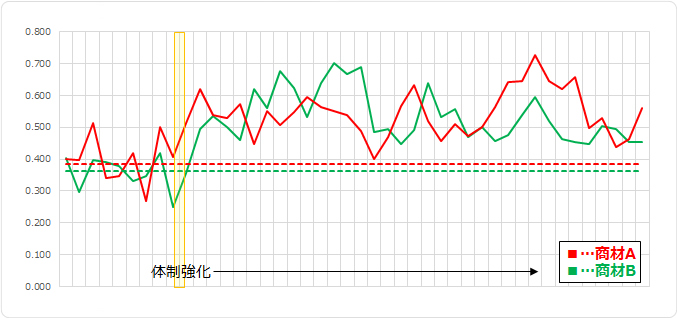
Nか月目の生存確率と95%信頼区間上下限値をプロットしてもいいでしょうが、グラフとしてはすごく見難くなるでしょう。
お勧めとしては、体制強化前後を比較するために、体制強化前のNか月目の生存確率の平均値(中央値)をプロットする手法です。そうすることで「強化によるインパクト」が可視化できるかと思います。
またグラフに売上もプロットして、相関性を表現しても良いと思います。そうすれば「Nか月目の生存確率をX%以上にすれば良いのではないか?」という仮説作りができるかと思います。
ただし、「ではそのためには何をすれば良いのか?」というのはセミノンパラメトリックでいくつかの説明変数を上げて分析しないといけないかもしれません。
そもそもデータを取っていない!という場合も考えられますので、まずは現場に見せて「説明変数は何だと思う?」と聞くのが良いのではないでしょうか。
他にどんな使い道があるのか?
段階定額制のような課金形態の場合、売上を伸ばし続けるためには以下の方程式を保ち続ける必要があります。
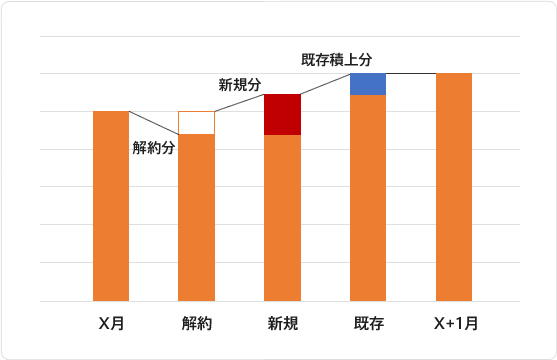
「今まで500円課金だったユーザーがなぜ1,990円課金に切り替わったのか?」という分析をする際、通常は説明変数を探してロジスティック回帰分析をするでしょう。
が、「もともとそのユーザーは1,990円課金をするつもりだった」という仮説を立て、1,990円課金切り替えをイベントに見なして、契約から何か月目でそのイベントが発生しがちなのか?という分析をするのも面白いかもしれません。
ちなみに、切り替えたユーザーとそうでないユーザーの解約率を分析して「やっぱ課金ユーザーの離脱率(解約率)は低いぜ」みたいな声が渋谷の何とかタワーから聞こえてくるとか、こないとか。
以上、お手数ですがよろしくお願いいたします。
参考図書

- 金 明哲
- 森北出版 2007-10-01

