2017年7月22日(土)に放映された、NHKスペシャル「AIに聞いてみた どうすんのよ!?ニッポン」が各所で波紋を呼んでいます。
その理由の1つとして「AIひろしは相関関係があるデータ項目を線で紐付けただけなのに、人間が勝手に因果関係だと解釈しているのではないか?」という声が多い点を挙げます。
しかし、放送を見ると、言うほど悪くなかったと思うのです。
近藤正臣さんが「因果関係は分からないけれど」と前提条件を説明したり、映像のテロップで「時系列の変化も分析」「『健康になった⇒病床数が減った』の順ではなく、『病床数が減った⇒健康になった』を導き出した」と注意書きが出たり。
一般市民としては「意外とちゃんとしてんちゃう?」感を抱きました。
そもそも時系列なデータのみで因果関係を証明するのは非常に難しく、統計的因果推論などの手法を用いて統計的に因果性を推論するしかありません。もし世間一般の皆さんが「その結果すら実際の意味での因果関係とは言えないだろ!」とご指摘されるのであれば、困ってしまう研究者の方は多くおられるのではないでしょうか。
そこで後追いですが、私も検証してみることにしました。以下、検証結果が続きますが、最初にまとめを掲載しておきます。
・前処理せずに都道府県別の相関係数を求めるとそこそこ高い結果が多い。
・単位根過程のデータが多いので前処理すると、使えないデータが多い(要意見求む)。
・前処理後、グレンジャー因果性検定を行った結果、3県だけ因果性を発見した。
・これでは「健康になりたければ病院を減らせ」とは言えないのではないか。もしかして「見せかけの回帰」に引っ掛かっているのではないか。
どのデータを検証するか?
NHKの今回の放送をまとめたWEBページに「AIの分析結果から読み解いた提言」が掲載されております。画像を引用するのは憚られるので、気になる方はリンク先をご参照ください。
この中で「病院数が減ればがん死亡者が減る」に着目しました。元々の提言が「健康になりたければ病院を減らせ」だったので、一番それに近しそうな関係に注目しています。
「病院数」と書かれていますが、番組が進行する過程で「病床数」だと分かっています。また「病床数(人口対)」と記載されていましたので、そのデータを探します。
データ元は厚生労働省医療施設調査・病院報告だと思われます。こちらについては、WEB上で1995年~2015年の21年分都道府県別のデータが公開されていました。残り9年分は入手できませんでした。
http://www.mhlw.go.jp/toukei/list/79-1a.html
続いて「がん死亡者数」ですが、それに該当すると考えられるデータは2つあります。いずれもデータ元は国立がん研究センターがん情報サービスが公開しています。
http://ganjoho.jp/reg_stat/statistics/stat/annual.html
1つは単純な「がん死亡者数」、もう1つは「がん年齢調整死亡率(人口10万人対)」です。
年齢調整死亡率とは、簡単に言えば高齢化による影響を取り除いた値です。高齢になるほどがんによる死亡率が高くなるため、高齢者が多い集団は高齢者が少ない集団よりがんの粗死亡率が高く現れるようになります。そこで、元データを加工してその影響を取り除いているわけですね。
病床数を人口10万人対で作成したのであれば、「がん年齢調整死亡率(人口10万人対)」を採択したのではないか?と考えます。そもそも単純な「がん死亡者数」であれば、高齢化という大きなトレンドがあるので除去は必須であり、すでに調整済みのデータを使うべきかとも考えます。
ちなみに、いずれもWEB上で1995年~2015年の21年分のデータが公開されていました。残り9年分は入手できませんでした。
何も考えずに散布図と相関係数を出してみる
まずは何も考えずにtableauにデータを食わせて、(47都道府県+全国)×21年間分の散布図を作成してみます。
相関がありそうな県、なさそうな県、ない交ぜですね。Tableau publicで作成していますので、デスクトップで見ておられる方はアプリケーションをDLしてグリグリ触ってみてください。
47都道府県+全国の、病床数とがん年齢調整死亡率の相関係数は以下の通りです。
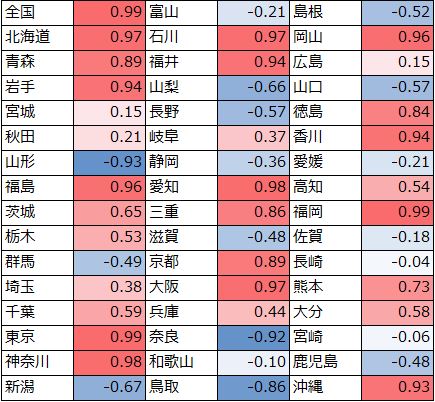
正の相関関係(相関係数0.4以上とした場合)にある都道府県は24都道府県+全国でした。
単位根過程か調べる
時系列データを用いた因果推論では、多変量自己回帰(VAR)モデルで読み解くことが多いです。したがって定常性の確保が重要だと考えます。
岩波データサイエンス6巻の「VARモデルによる因果関係の推論」から引用しますと、定常性とは「時系列自身の過去との相関が、どれだけ離れた過去かという時間差には依存しても、どこで相関を測っているかという時点には依存しないという要請」であり、「時系列の自己相関が非常に高い場合(特に何らかの意味でトレンドが存在する場合)は、時系列どうしの回帰(多変量時系列解析)から得られるパラメータ推定値の解釈は、特別な注意が必要であることがよく知られている」とあります。
つまり、時系列データを用いて分析を行い、意味ある結果を得るためには、事前にトレンドの除去を行わなければならない可能性があります。その除去自体が必要か不要かを判断するのが単位根検定です。
ものすごく簡単に言うと、分析する前に「おまじない」が必要か調べて、「必要」って言われたらおまじないをかけます。
まず、対象となる「病床数(人口10万人対)」と「がん年齢調整死亡率(人口10万人対)」が、それぞれ単位根過程にないかどうか確認します。
今回、RでAugmented Dickey-Fuller検定を行ったところ、以下のような結果になりました。(P値は0.05で見ています)
茨城、石川、福井、奈良、愛媛、福岡、佐賀以外は単位根過程にある
・がん年齢調整死亡率(人口10万人対)
山口、高知、長崎 以外は単位根過程にある
殆どの都道府県の時系列データにおいて「おまじない」が必要ですね…。
両方の変数で、差分をとった上で再び単位根検定を行い、「単位根過程である」とする帰無仮説が棄却されたデータで再び散布図を作成してみました。(これ以外の「おまじない」もあると思います。他手法ぜひご指導いただければ幸いです)
また、差分などをもってもトレンドを取り除けなかった北海道、青森、山形、茨城、栃木、群馬、埼玉、千葉、東京、神奈川、石川、静岡、三重、京都、兵庫、奈良、和歌山、山口、徳島、香川、高知、宮崎の22都道府県は以降の分析対象から除外しました。北関東、関西、四国ほぼ全滅です。(対数変換後差分などでも対応できませんでした。こちら手法詳しい方ぜひご指導いただければ幸いです)
ってか、こんなに対象外の都道府県がある時点でアレですね…。21時点しかデータがないのも厄介だ…。せめて月単位であれば…。
単位根過程に無いデータをtableauに食わせて、先ほどと同じように散布図を作成してみます。
単位根過程に無い24府県の病床数とがん年齢調整死亡率の相関係数は以下の通りです。
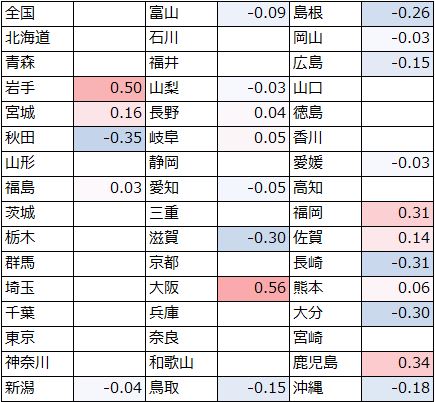
ま、やっぱそうなりますよね…。正の相関関係(相関係数0.4以上とした場合)にある府県は岩手と大阪でした。
もし単位根過程にあるデータのみで相関を判断していたとなると、それは「見せかけの回帰」的な話でしょうか。
グレンジャー因果性検定を行う
映像では「ディープラーニングを用いている」と説明があったので、おそらくリカレントニューラルネットワークを採択しているのではないか?と仮説を抱いています。当方にそこまでの技術力が無いため、以下の教科書を参考にした結果、グレンジャー因果性検定を行うこととしました。

- 岩波データサイエンス Vol.6
- 岩波データサイエンス刊行委員会
- 岩波書店 2017-06-23
ある時系列データXを予測するのに、他の時系列データYの過去の値が役立つなら、「YからXに対してグレンジャーの意味で因果性がある」と言います。要は「Yのデータを使えばXの予測ができますよ。それってYがXに何らか関係しているということですよね?」という意味で、データだけで因果関係を推論するメジャーな方法です。
今回、24府県毎にGranger Causality検定を行いました。「病床数が減ればがん年齢調整死亡率が減る」とのことなので「病床数からがん年齢調整死亡率への因果性は無い」という帰無仮説が5%水準で棄却できるかどうか調べます。
当たり前ではありますが、各府県単位である程度あてはまりに満足できるVARモデルを選択しているので、府県によってはVARモデルのラグが異なります。
どなたかがAIの仕組みについて「5年ほどの期間のズレがあっても~」と発言されていましたが、もしかしてVARモデルのラグの話をしているのかな?と思っていました。
結果、秋田(lag3)、長野(lag4)、佐賀(lag5)は、グレンジャーの意味で因果性がある県だと判断できました。(P値は0.05で見ています)
この結果から鑑みるに、「そういう地域はあるのかもしれないけど、病院数を減らせばガン死亡者数は減るとまでは言い切れないんじゃない?」という声が脳内に響いております。
ちなみに色々期間を操作したのですが、病院数が減ればがん死亡者数が減ってるとは言えない…かな…。
もちろん、この結果を受けて秋田、長野、佐賀では「病床数からがん年齢調整死亡率への因果関係はある」とは言い切れません。データとしてそういう結果になっているだけで、ここから実際の検証が必要になっていきます。
したがって、なぜ取材班は北海道・夕張に足を運んだのか?が謎なんです。
またグレンジャー因果性検定を実施する前段のデータ処理については単位根検定だけでなく共和分検定など、さらに要確認な場合があります。興味のある方は岩波データサイエンス6巻を手に取ってみてください。
データ分析ちょっとよく分からない!という方は、「今回対象となるデータだけで因果性があるとAIひろしは判断したけど、それってどういうロジックなんだろうね?不思議だね」と捉えて頂ければ幸いです。
今回のまとめ
AIひろし自体は、私は好きなんです。
理由はNHKがわざわざ日本中のオープンデータを30年分、都道府県レベルで集めてくれたからです。さすがNHK、中央省庁もデータ提供してくれるんだ!と感心しました。前処理をしてくれれば、結構使えると思うのです。
今回、AIのアウトプットをどのように提示するのかという課題が浮き彫りになりましたよね。
病院数が減ればがん死亡者数が減る、これはAIひろしの「発見」です。
AIのアウトプットを受けて人間が「健康になりたければ病院を減らせ」と意訳したのですが、さすがにそれは言い過ぎじゃない?と思うわけです。戸田奈津子じゃないんだからと思うわけです。
また、後追い研究者向けに「変数」のタイトルはちゃんとして欲しいと思いました。病院数と病床数はぜんぜん違うからです。
結局は「人間の判断次第で結果なんて、どうにでも変わる」ということだけが分かったNHKスペシャル「AIに聞いてみた どうすんのよ!?ニッポン」だったのではないかと思います。
最後に、夕張の皆さんがバナナを食べている件ですが、家計調査の1世帯当たり年平均支出 (二人以上の世帯)を調べると、フルーツの中でもっとも食べられていて、もっともお金を払っているのがバナナなだけです。
要は偶然かと思います。他の多くのフルーツは包丁使わないといけないので、バナナとみかん(柑橘系)は鉄板です。
あの場所で「みかん食べる人ー?」って聞いたら、同じように全員手を挙げたんじゃないでしょうか。
人は、あたかも偶然の出来事に目を向けて、そこに理由を求めようとします。それこそ相関と因果だと僕は思うのですが、皆さんはいかが思われますか。
以上、お手数ですがよろしくお願いいたします。
今回使ったデータについて
病床数のデータについてはこちら
がん死亡者数のデータについてはこちら
今回は実施しませんでしたが10代前半人口のデータ(総務省統計局より)についてはこちら